PAIRE ORDONNÉE

L16.p03. S’il y a une formule que j’ai répétée ces jours-ci, ces temps-ci avec insistance, c’est celle qui enracine la détermination du sujet en ceci qu’un signifiant le représente, le représente pour un autre signifiant.

Cette formule a l’avantage d’insérer dans une connexion la plus simple, la plus réduite, celle d’un signifiant 1, S1, à un signifiant 2, S2, SI à S2 ; ce de quoi il nous faut partir pour ne pas perdre, ne plus pouvoir perdre un seul instant la dépendance du sujet. Le rapport de ce signifiant 1 à ce signifiant 2, tous ceux – et il n’est pas du tout rare de pouvoir l’espérer, à partir d’un certain moment – tous ceux qui ont quelque audition de ce qu’il en est en logique, dans ce qu’il en est proprement dans la théorie des ensembles, de ce qu’on appelle une paire ordonnée, je ne puis ici qu’en donner l’indication quitte à ce que, sur telle demande qui me vienne, j’en donne plus tard un commentaire. Cette référence théorique est néanmoins importante à être ici attachée.

L16.p.41. L16 03.P.15 Mais nous avons autre chose à faire que de la logique mathématique. Notre rapport à l’Autre est un rapport plus brûlant et le fait de 41 savoir si ce qui surgit du seul fait de la demande que l’Autre contient déjà en quelque sorte, tout ce autour de quoi elle s’articule, s’il s’agissait seulement de discours, autrement dit s’il y avait un dialogue, ce que très précisément, à la fin de l’année dernière, j’ai ici proféré qu’il n’y est pas ce dialogue, si donc cet Autre pouvait être conçu comme le code fermé, celui sur le clavier duquel il n’y a qu’à appuyer pour que le discours s’institue sans faille, pour que le discours puisse s’y totaliser, c’est ceci que, de cette façon rudimentaire et, en quelque sorte en marge de la théorie des ensembles, j’interroge. J’aurais pu mettre à la place de ce S un petit b, comme cela, vous vous seriez aperçu qu’il s’agit du b, a, ba. Nous sommes au b, a, ba de la question et dès le b, a, ba, vous allez voir comment elle se creuse et ceci topologiquement; si c’est ainsi que nous avons posé la question, il est clair que ce qui est A dans la paire ordonnée qui constitue cet ensemble est pris pour identique au A qui le désigne. Nous allons donc écrire ainsi, rapport de S avec S en rapport avec grand A, S – (S – A).

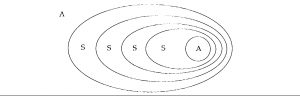
Je substitue à ce A ce que ce A est en tant qu’il est le signifiant de l’ensemble constitué par le rapport de S à A, rapport de paire ordonnée. Ceci est tout à fait usuel dans tout développement d’une théorie des ensembles dont le fondement même est ceci, que tout élément est supposé pouvoir être ensemble lui-même. Vous voyez donc ce qui se produit ; à partir de ce procès nous allons avoir une série de – je ne sais pas ce que c’est que ces cercles que je dessine, ils nous ont servi à faire fonctionner l’ensemble et sa désignation comme telle -, nous avons une répétition indéfinie du S sans que nous puissions à la fin jamais arrêter le recul, si je puis dire, du grand A.

Ne vous mettez pas dans la tête pourtant qu’il se réduit, qu’il s’évanouit, si je puis dire, spatialement, que d’aucune façon ici soit indiqué quelque chose qui constitue, qu’il soit de l’ordre d’une réduction infinitésimale d’une distance, ou de quelque passage à la limite. Il ne s’agit que de l’insaisissabilité, encore qu’il reste toujours le même, de ce A comme tel. Ce caractère insaisissable n’est sûrement pas pour nous surprendre puisque nous en avons fait de ce grand A le lieu de l’Urverdrüngung.

Car essayons maintenant, ce sujet, de le tenir, où il est représenté. Tâchons de l’extraire ce S, ce signifiant qui le représente, de l’ensemble constitué par la paire ordonnée. C’est là qu’il vous sera très simple de retomber sur un terrain connu, c’est le paradoxe de Russell. Que faisons­-nous ici ? sinon extraire de l’ensemble A ceux des signifiants dont nous pouvons dire qu’ils ne se contiennent pas eux-mêmes. Il suffit – et je vous laisse aller chercher dans les premières pages de n’importe quelle théorie, naïve ou pas, des ensembles – il suffit que vous vous y reportiez pour savoir que, de la même façon que c’est parfaitement illustré dans l’articulation du sophisme, la classe de tous les catalogues qui ne se contiennent pas eux-mêmes ne saurait d’aucune façon se situer sous forme d’ensemble pour la bonne raison qu’elle ne peut d’aucune façon se reconnaître dans les éléments déjà inscrits de cet ensemble. Elle en est distincte, j’ai déjà rebattu ce thème, il est courant, il est trivial. Il n’y a aucune façon d’inscrire dans un ensemble ce quelque chose que vous pourriez en extraire en le désignant comme l’ensemble des éléments qui ne se contiennent pas eux-mêmes.

Entrons dans le vif parce que nous sommes en retard et reprenons en rappelant sur quoi, en somme, se centraient nos derniers propos, sur l’Autre en somme, sur ce que j’appelle le grand Autre. J’ai terminé en promouvant certains schémas, avertissant, je pense, assez qu’ils n’étaient pas à prendre uniquement sur leur aspect plus ou moins fascinant, mais à rapporter à une articulation logique, celle, proprement, qui se compose de ce rapport d’un signifiant à un autre signifiant, S₁ →S₂, que j’ai essayé d’articuler pour en tirer les conséquences en partant de la fonction, élaborée dans la théorie des ensembles, de la paire ordonnée. Du moins est-ce sur ce fondement logique que j’ai essayé la dernière fois de vous faire sentir ce quelque chose qui a une pointe, une pointe autour de quoi tourne l’intérêt – l’intérêt pour tous j’espère -, l’intérêt qu’il y a à ce que ceci s’articule bien, que l’Autre, ce grand Autre, A, dans sa fonction comme je l’ai déjà approchée, l’Autre n’enferme nul savoir dont il se puisse présumer, disons, qu’il soit un jour absolu.

Le sort de l’Autre est donc suspendu, je ne dirai pas à la question, je ne dirai pas à ma question, à la question que pose l’expérience psychanalytique. Le drame est que quel que soit le sort que lui réserve cette mise en question, ce que la même expérience démontre, c’est que c’est de son désir à l’Autre que je suis – dans les deux sens merveilleusement homonymiques en français de ces deux mots – que je suis la trace. C’est d’ailleurs précisément en cela qu’au sort de l’Autre je suis intéressé. Alors, il nous reste un quart d’heure et le petit mot que j’ai reçu s’énonce ainsi : “Mercredi dernier vous avez mis en rapport sans préciser la paire ordonnée et un signifiant représente le sujet pour un autre signifiant (S → S)”. C’est tout à fait vrai. C’est pour ça que sans doute mon correspondant a mis dessous une barre, et au­ dessous de la barre, “pourquoi?”, avec un point d’interrogation. En-dessous de “pourquoi ?” une autre barre, puis, marqué par deux gros points ou plus exactement deux petits cercles remplis de noir. “Quand la paire ordonnée est introduite en mathématique, il faut un coup de force pour la créer.”

A ceci, je reconnais que la personne qui m’a envoyé ce papier sait ce qu’elle dit, c’est-à-dire qu’elle a au moins une ombre, qui est probablement plus encore, d’instruction mathématique. C’est  L16 04.P11 tout à fait vrai. On commence par articuler la fonction de ce que c’est qu’un ensemble et si on n’y introduit pas, en effet, la fonction de la paire ordonnée par cette sorte de coup de force qu’on appelle en logique un axiome, eh bien !, il n’y a rien de plus à en faire que ce que vous avez d’abord défini comme ensemble. Entre parenthèses, ajoute-t-on – soit direct, soit indirect – l’ensemble a deux éléments. “Le résultat de ce coup de force est de créer un signifiant qui remplace la coexistence de deux signifiants”. C’est tout à fait exact. Deuxième remarque. “La paire ordonnée détermine ces deux composants, tandis que dans la formule un signifiant représente le sujet pour un autre signifiant, il serait étonnant qu’un sujet détermine deux signifiants.” Je n’ai plus qu’un quart d’heure et pourtant j’espère avoir le temps d’éclairer comme il faut, car ce n’est pas difficile, ce que j’ai énoncé la dernière fois, qui prouve que je ne l’ai pas suffisamment bien énoncé puisque quelqu’un, en ces termes, comme vous le voyez des plus sérieux, m’interroge.

Je vais donc écrire au tableau – quel que soit l’inconvénient qu’on m’a signalé déjà la dernière fois de l’usage de ce tableau, qui devrait être placé là pour que tout le monde le voie, ce que j’écris, et ça ne sera pas encore pour aujourd’hui, au regard des difficultés qu’a conditionnée ma venue en retard -, ceci: < S1, S2>; à aucun moment je n’ai subsumé dans un sujet la coexistence de deux signifiants. Si j’introduis la paire ordonnée que, comme le sait sûrement mon interlocuteur, j’écris par exemple ainsi, <Sl,S2>, ces deux signes se trouvent par un bon hasard être les deux morceaux de mon poinçon quand ils se rejoignent, ces deux signes ne servent dans l’occasion qu’à très précisément écrire que ceci est paire ordonnée. La traduction sous forme d’ensemble, je veux dire articulé dans le sens du bénéfice qu’on attend du coup de force en question, c’est de traduire ceci dans un ensemble dont les deux éléments, les éléments dans un ensemble étant toujours eux-mêmes ensemble, vous voyez se répéter le signe de la parenthèse {{S1},{S1,S2}} deuxième élément de cet ensemble {S1 , S2}, une paire ordonnée est un ensemble qui a deux éléments, un ensemble formé du premier élément de la paire et un second ensemble ; ce sont donc l’un et l’autre des sous-ensembles formés des deux éléments de la paire ordonnée. L16.04.P13

Loin que le sujet ici d’aucune façon subsume les deux signifiants en question, vous voyez, je suppose, combien il est aisé de dire que le signifiant Si, ici, ne cesse de représenter le sujet comme ma définition le signifiant représente un sujet pour un autre signifiant l’articule, cependant que le second sous-ensemble présentifie ce que mon correspondant appelle cette “coexistence”, c’est-à-dire dans sa forme la plus large cette forme de relation qu’on peut appeler “savoir”. La question que je pose à ce propos et sous sa 55 forme la plus radicale, si un savoir est concevable qui réunisse cette conjonction des deux sous-ensembles en un seul, d’une façon telle qu’ils puissent être sous le nom de A, du grand Autre, identiques à la conjonction telle qu’elle est ici articulée en un savoir des deux signifiants en question.

L16 05 P11 “. A la demande de “qui est je”, la structure même répond par ce refus signifiant de A, tel que je l’ai inscrit dans le fonctionnement de ce graphe, de même ce qui est ici le “Tu”, l’institue d’une convergence entre la demande la plus radicale, celle qui nous est faite à nous analystes, la seule qui soutienne, au dernier terme, le discours du sujet ; “je viens ici pour te demander”, au premier temps, c’est bien de “qui je suis” qu’il s’agit si c’est au niveau du “qui est je” qu’il est répondu, c’est bien sûr que c’est la nécessité logique qui donne là ce recul.

Convergence, donc, de cette demande et, ici, quelque chose d’une promesse, ce quelque chose qui, en S2 est l’espoir du rassemblement de ce …

“Je”. C’est bien ce que, dans le transfert j’ai appelé du terme le sujet supposé savoir, c’est-à-dire cette prime conjonction, S lié à S2, en tant que, comme je l’ai rappelé la dernière fois, dans la paire ordonnée, c’est lui, c’est cette conjonction, c’est ce nœud qui fonde ce qui est savoir.

Qu’est-ce donc à dire ? Si le “je” n’est sensible que dans ces deux pôles, eux, divergents qui l’un s’appelle ce que ici j’articule comme le non, le refus qui donne forme au manque de la réponse, et ce quelque chose d’autre qui est là articulé comme petit s de grand A, cette signification quelle est-elle ? Car n’est-il pas sensible que tout ce discours que je file pour donner l’armature au “je” de l’interrogation dont s’institue cette expérience, n’est-il pas sensible que je le poursuis en laissant en-dehors, au moins jusqu’à ce point où nous arrivons ici, aucune signification ?

L’un tel que nous le prenons ici est d’un autre ordre que cet Un élaboré par la méditation platonicienne. Il est clair que, pour ceux qui déjà m’ont entendu cette année, ce rapport de l’un à l’Autre ne va à rien de moins qu’à rappeler, qu’à faire sentir la fonction de la paire ordonnée dont vous avez vu au passage quel est le rôle majeur dans l’introduction de ce qu’on appelle bizarrement la théorie des ensembles, car tout le monde semble s’accommoder fort aisément de ces ensembles, au pluriel, alors que c’est justement une question, et très vive quoique non totalement tranchée encore, si l’on peut les mettre au pluriel. En tout cas ce n’est pas si aisé si la question reste ouverte de savoir si l’on peut considérer d’aucune façon qu’un élément peut appartenir à deux ensembles différents en restant le même. C’est une petite parenthèse destinée à vous rappeler que ça n’est pas sans constituer une très forte innovation logique que tout ce qui se rapporte à ce que j’appellerai l’ensemblissement – pour des raisons de consonance, j’aime mieux ça que ensemblement -, quoiqu’il arrive que la théorie des ensembles s’ensable de temps en temps. Mais elle se réensemblit fort allègrement. Ce n’est évidemment qu’en marge d’une telle référence que je voudrais vous rappeler cette innovation tout à fait radicale que la théorie des ensembles constitue d’introduire ce pas, et littéralement à son principe, que ce qu’il s’agit de ne pas confondre, c’est en aucun cas un élément quelconque avec l’ensemble qui pourtant ne l’aurait que pour seul élément. Ce n’est pas du tout pareil. Et c’est là le pas d’innovation logique qui doit nous servir exactement à introduire comme il convient cet Autre problématique dont je viens d’interroger pourquoi nous lui donnerions cette valeur notoire : l’Autre.

Or ceci est capital car nous allons le toucher immédiatement du doigt sous la forme suivante, c’est qu’à énumérer les sous-ensembles de notre Autre ici réduit à sa fonction la plus simple, à savoir d’être un ensemble portant le 1, de ce signifiant nécessaire comme étant celui auprès duquel va se représenter de l’un à l’Autre le un du sujet; vous verrez tout à l’heure dans quelles limites il est légitime de réduire ces deux S, S, et S, à un même un. C’est bien ce qui est l’objet de nos remarques d’aujourd’hui. Il est clair qu’à interroger le 1 inscrit dans le champ défini comme Autre, comme ensemble comme tel, nous aurons comme sous-ensembles 1 et ceci qui est la façon d’écrire l’ensemble vide. Illustration la plus simple de ceci que j’ai rappelé que les sous-ensembles constituent une collection numériquement supérieure à celle des éléments qui définissent un ensemble.

Est-ce qu’il est nécessaire d’insister, que vous voyez ici se reproduire sous la forme de cette double parenthèse qui est bien effectivement la même que celle de la ligne qui désigne ici A, exactement l’identité de ce A comme ensemble vide, en ces deux points du schéma qui le reproduisent. Voici donc évoqué, dès que au champ de l’Autre, quelque chose peut s’inscrire d’aussi simple que le trait unaire, dès que ceci est conçu, du même mouvement surgit, par la vertu de l’ensemble, la fonction de la paire ordonnée. Car il suffit de voir que dès lors les deux 1 qui peuvent s’inscrire l’un ici comme premier élément de l’ensemble et l’autre à remplir le second ensemble vide, s’il est possible de s’exprimer ainsi car comme ensemble vide, c’est le même, ces deux 1 se distingueront d’une appartenance différente.

C’est bien là où gît la vertu non rencontrée jusqu’alors de ce de l’un à l’Autre, mine de rien, d’où nous sommes partis tout à l’heure pour y rappeler ce qu’a de spécifique la relation qui nous intéresse et qui motive cette année notre titre D’un Autre à l’autre. C’est pour autant que tout ce qui est de ce qui fait notre expérience ne peut que tourner, retourner et toujours revenir se pointer autour de la question de la subsistance du sujet, toujours axe, axiomatique indispensable à ne jamais perdre ce à quoi nous avons à faire dans le concret de la façon la plus efficace, à savoir que si cet axe et cet axiome n’est pas conservé nous entrons dans la confusion, celle qui s’étale aux derniers temps dans tout ce qui se fait de l’énoncé de l’expérience analytique et spécialement à l’intégration de plus en plus envahissante de cette fonction dite The Self qui fait prime dans les articulations présentes de l’analyse anglo-américaine.