THÉORIE DES ENSEMBLES
L16.p.41. L16 03.P.15 Mais nous avons autre chose à faire que de la logique mathématique. Notre rapport à l’Autre est un rapport plus brûlant et le fait de 41 savoir si ce qui surgit du seul fait de la demande que l’Autre contient déjà en quelque sorte, tout ce autour de quoi elle s’articule, s’il s’agissait seulement de discours, autrement dit s’il y avait un dialogue, ce que très précisément, à la fin de l’année dernière, j’ai ici proféré qu’il n’y est pas ce dialogue, si donc cet Autre pouvait être conçu comme le code fermé, celui sur le clavier duquel il n’y a qu’à appuyer pour que le discours s’institue sans faille, pour que le discours puisse s’y totaliser, c’est ceci que, de cette façon rudimentaire et, en quelque sorte en marge de la théorie des ensembles, j’interroge. J’aurais pu mettre à la place de ce S un petit b, comme cela, vous vous seriez aperçu qu’il s’agit du b, a, ba. Nous sommes au b, a, ba de la question et dès le b, a, ba, vous allez voir comment elle se creuse et ceci topologiquement; si c’est ainsi que nous avons posé la question, il est clair que ce qui est A dans la paire ordonnée qui constitue cet ensemble est pris pour identique au A qui le désigne. Nous allons donc écrire ainsi, rapport de S avec S en rapport avec grand A, S – (S – A).
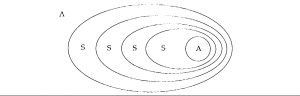
Je substitue à ce A ce que ce A est en tant qu’il est le signifiant de l’ensemble constitué par le rapport de S à A, rapport de paire ordonnée. Ceci est tout à fait usuel dans tout développement d’une théorie des ensembles dont le fondement même est ceci, que tout élément est supposé pouvoir être ensemble lui-même. Vous voyez donc ce qui se produit ; à partir de ce procès nous allons avoir une série de – je ne sais pas ce que c’est que ces cercles que je dessine, ils nous ont servi à faire fonctionner l’ensemble et sa désignation comme telle -, nous avons une répétition indéfinie du S sans que nous puissions à la fin jamais arrêter le recul, si je puis dire, du grand A.
Ne vous mettez pas dans la tête pourtant qu’il se réduit, qu’il s’évanouit, si je puis dire, spatialement, que d’aucune façon ici soit indiqué quelque chose qui constitue, qu’il soit de l’ordre d’une réduction infinitésimale d’une distance, ou de quelque passage à la limite. Il ne s’agit que de l’insaisissabilité, encore qu’il reste toujours le même, de ce A comme 42 tel. Ce caractère insaisissable n’est sûrement pas pour nous surprendre puisque nous en avons fait de ce grand A le lieu de l’Urverdrüngung.
44 Car essayons maintenant, ce sujet, de le tenir, où il est représenté. Tâchons de l’extraire ce S, ce signifiant qui le représente, de l’ensemble constitué par la paire ordonnée. C’est là qu’il vous sera très simple de retomber sur un terrain connu, c’est le paradoxe de Russell. Que faisons-nous ici ? sinon extraire de l’ensemble A ceux des signifiants dont nous pouvons dire qu’ils ne se contiennent pas eux-mêmes. Il suffit – et je vous laisse aller chercher dans les premières pages de n’importe quelle théorie, naïve ou pas, des ensembles – il suffit que vous vous y reportiez pour savoir que, de la même façon que c’est parfaitement illustré dans l’articulation du sophisme, la classe de tous les catalogues qui ne se contiennent pas eux-mêmes ne saurait d’aucune façon se situer sous forme d’ensemble pour la bonne raison qu’elle ne peut d’aucune façon se reconnaître dans les éléments déjà inscrits de cet ensemble. Elle en est distincte, j’ai déjà rebattu ce thème, il est courant, il est trivial. Il n’y a aucune façon d’inscrire dans un ensemble ce quelque chose que vous pourriez en extraire en le désignant comme l’ensemble des éléments qui ne se contiennent pas eux-mêmes.
47 Entrons dans le vif parce que nous sommes en retard et reprenons en rappelant sur quoi, en somme, se centraient nos derniers propos, sur l’Autre en somme, sur ce que j’appelle le grand Autre. J’ai terminé en promouvant certains schémas, avertissant, je pense, assez qu’ils n’étaient pas à prendre uniquement sur leur aspect plus ou moins fascinant, mais à rapporter à une articulation logique, celle, proprement, qui se compose de ce rapport d’un signifiant à un autre signifiant, S1 à S2, que j’ai essayé d’articuler pour en tirer les conséquences en partant de la fonction, élaborée dans la théorie des ensembles, de la paire ordonnée. Du moins est-ce sur ce fondement logique que j’ai essayé la dernière fois de vous faire sentir ce quelque chose qui a une pointe, une pointe autour de quoi tourne l’intérêt – l’intérêt pour tous j’espère -, l’intérêt qu’il y a à ce que ceci s’articule bien, que l’Autre, ce grand Autre, A, dans sa fonction comme je l’ai déjà approchée, l’Autre n’enferme nul savoir dont il se puisse présumer, disons, qu’il soit un jour absolu.
293 L’un tel que nous le prenons ici est d’un autre ordre que cet Un élaboré par la méditation platonicienne. Il est clair que, pour ceux qui déjà m’ont entendu cette année, ce rapport de l’un à l’Autre ne va à rien de moins qu’à rappeler, qu’à faire sentir la fonction de la paire ordonnée dont vous avez vu au passage quel est le rôle majeur dans l’introduction de ce qu’on appelle bizarrement la théorie des ensembles, car tout le monde semble s’accommoder fort aisément de ces ensembles, au pluriel, alors que c’est justement une question, et très vive quoique non totalement tranchée encore, si l’on peut les mettre au pluriel. En tout cas ce n’est pas si aisé si la question reste ouverte de savoir si l’on peut considérer d’aucune façon qu’un élément peut appartenir à deux ensembles différents en restant le même. C’est une petite parenthèse destinée à vous rappeler que ça n’est pas sans constituer une très forte innovation logique que tout ce qui se rapporte à ce que j’appellerai l’ensemblissement – pour des raisons de consonance, j’aime mieux ça que ensemblement -, quoiqu’il arrive que la théorie des ensembles s’ensable de temps en temps. Mais elle se réensemblit fort allègrement. Ce n’est évidemment qu’en marge d’une telle référence que je voudrais vous rappeler cette innovation tout à fait radicale que la théorie des ensembles constitue d’introduire ce pas, et littéralement à son principe, que ce qu’il s’agit de ne pas confondre, c’est en aucun cas un élément quelconque avec l’ensemble qui pourtant ne l’aurait que pour seul élément. Ce n’est pas du tout pareil. Et c’est là le pas d’innovation logique qui doit nous servir exactement à introduire comme il convient cet Autre problématique dont je viens d’interroger pourquoi nous lui donnerions cette valeur notoire : l’Autre.
C’est ici, justement, qu’il s’agit de comprendre que cette vérité émise est là suspendue, prise entre deux registres qui sont ceux dont précisément j’ai posé les deux bornes dans les deux termes qui figurent au titre de mon Séminaire cette année. Car cet ou bien, référence au champ où le discours du sujet prendrait consistance, c’est-à-dire au champ de l’Autre qui est celui que j’ai défini pour ce lieu où tout discours au moins se pose pour pouvoir s’offrir à ce qui est ou non sa réfutation, qu’il puisse se démontrer, et sous la forme la plus simple – vous m’excuserez de n’avoir pas le temps de le faire aujourd’hui -, que le problème est totalement déplacé de savoir s’il est ou non un Dieu qui garantisse, comme pour Descartes, le champ de la vérité ; il nous suffit qu’il puisse se démontrer qu’au champ de l’Autre il n’y a pas de possibilité d’entière consistance du discours, et ceci, j’espère pouvoir, la prochaine fois, vous l’articuler précisément en fonction de l’existence du sujet. Je l’ai déjà une fois écrit très rapidement au tableau. C’est une démonstration très aisée à trouver au premier chapitre de ce qu’on appelle la théorie des ensembles, mais encore faut-il, au moins pour une part des oreilles qui sont ici, montrer en quoi il est pertinent d’introduire dans l’élucidation de la fonction d’un discours comme celui qui est le nôtre, à 17 nous analystes, de quelque façon extraite d’une logique dont ce serait tout à fait un tort que de croire que c’est une façon de l’exclure dans l’amphithéâtre voisin que de l’appeler logique mathématique. Si nulle part dans l’Autre ne peut être assurée d’aucune façon la consistance de ce qui s’appelle vérité, où donc est-elle sinon à ce qu’en réponde cette fonction du a. Aussi bien n’ai-je pas déjà à quelque autre occasion émis ce qu’il en est du cri de la vérité. “Moi, la vérité, ai-je écrit, je parle, et je suis pure articulation émise pour votre embarras”.
Cette formule a l’avantage d’insérer dans une connexion la plus simple, la plus réduite, celle d’un signifiant 1, S1, à un signifiant 2, S2, SI à S2 ; ce de quoi il nous faut partir pour ne pas perdre, ne plus pouvoir perdre un seul instant la dépendance du sujet. Le rapport de ce signifiant 1 à ce signifiant 2, tous ceux – et il n’est pas du tout rare de pouvoir l’espérer, à partir d’un certain moment – tous ceux qui ont quelque audition de ce qu’il en est en logique, dans ce qu’il en est proprement dans la théorie des ensembles, de ce qu’on appelle une paire ordonnée, je ne puis ici qu’en donner l’indication quitte à ce que, sur telle demande qui me vienne, j’en donne plus tard un commentaire. Cette référence théorique est néanmoins importante à être ici attachée.
Pourtant, ceci que j’appelle mon discours ne date pas d’hier; je veux dire que, comme je vous l’ai annoncé la dernière fois, il y a quelque chose au bord de quoi notre chemin nous mène, c’est ce qui déjà est construit au niveau même de l’expérience et je dirais, du travail, du travail qui consiste à faire rentrer dans mon discours, dans un “je dis” provoquant ceux qui veulent bien franchir l’obstacle que rencontre ce seul fait que ce discours, à un moment, ait été commencé au sein d’une institution qui, comme telle, était faite pour le suspendre. Et ce discours, j’ai essayé de le situer, de le construire dans sa relation fondamentale au rapport du savoir dans quelque chose que certains de ceux qui ont pu ouvrir mon livre ont pu trouver à une 34 certaine page dessiné sous le nom de graphe – dix ans ! Dix ans déjà que cette opération a abouti à sa venue au jour dans le Séminaire de 1957-58 sur Les Formations de l’Inconscient. Et pour bien marquer les choses dans le vif de ce dont il s’agit, je dirai que c’est par un commentaire du Witz, du mot d’esprit, comme Freud s’exprime, du mot d’esprit, donc, dis-je, que cette construction a commencé.
Contentons-nous, c’est un artifice d’exposition – je n’ai point ici à le dissimuler – qui m’évite une introduction par la voie de la théorie des ensembles et le rappel – s’il fallait que je le fasse, il faudrait que je le fasse un tant soit peu articulé – le rappel de ce fait qu’au premier pas, cette théorie trébuche sur un paradoxe, celui qu’on appelle le paradoxe de Russell, c’est à savoir que faire dans une certaine définition qui est celle des ensembles, à savoir de ce qui est au plus près de la relation signifiante, une relation de connexion. Rien d’autre n’est indiqué encore dans ce qu’articule la première définition de la fonction du signifiant, si ce n’est que le signifiant 1, dans un rapport, que nous pouvons définir comme nous voulons, le terme le plus simple sera celui d’appartenance, rapport d’un signifiant à un autre signifiant, dans ce rapport, avons-nous dit, il représente le sujet,
S1 à S2. Cette connexion si simple et qui suffit à nous indiquer, si tant d’autres traits ne nous l’indiquaient pas, à nous indiquer que de la logique mathématique, comme maints linguistes s’en sont aperçus, c’est la théorie des ensembles qui se trouve le plus à portée d’en traiter, je ne dis pas 40 de la formaliser, de traiter de cette connexion. Je vous rappelle, pour ceux qui en ont un petit peu entendu parler, que le premier pas qui se rencontre c’est qu’à cette seule condition de considérer comme une classe – et ceci même se démontre – tout élément d’une telle connexion en tant qu’on peut écrire qu’il ne s’appartient pas à lui-même, va entraîner un paradoxe. Je le répète, cette introduction, je ne fais ici qu’en indiquer la place, la développer nous ferait rebondir sur des énoncés encore bien plus singuliers.
-achetez Naissance de la psychanalyse, comme a été traduit le recueil de lettres à Fliess auquel était jointe cette Entwurf, et vous verrez bien qu’en effet ce dont Freud a trouvé un support aisé dans ce qui était alors à la portée de sa main du fait que de cela aussi on venait de faire la découverte, à savoir l’articulation neuronique, ce n’était rien d’autre que l’articulation sous la forme la plus élémentaire des signifiants et des relations qui peuvent se fixer à la façon dont, de nos jours un même schéma qui aurait la même forme, achetez le dernier petit bouquin venu, ou plutôt achetez Théorie axiomatique des ensembles par M. Krivine, vous y verrez exactement les schémas de Freud à ceci près que ce dont il s’agit, ce sont des petits schémas orientés à peu près ainsi, et qui sont nécessaires pour nous faire comprendre ce qu’il en est de la théorie des ensembles. Ceci veut dire que tout point, dans la mesure où il est relié par une flèche à un autre, est considéré dans la théorie des ensembles comme élément de l’autre ensemble, et vous verrez qu’il ne s’agit de rien de moins que ce qui est nécessaire pour donner une articulation correcte à ce qu’il y a de plus formel pour donner son fondement à la théorie mathématique , et déjà là vous verrez, à simplement lire les premières lignes, à savoir ce que comporte chaque pas axiomatique franchi, les véritables nécessités prises sous l’angle formel dans ce qu’il en est de l’articulation signifiante prise à son niveau le plus radical qui est ceci notamment de particulièrement exemplaire que la notion qui s’y définit d’une partie concernant ses éléments, éléments qui sont toujours des ensembles, la façon dont on dit qu’un de ces éléments est contenu dans un autre, repose sur des définitions formelles qui sont telles qu’elles se distinguent, qu’elles ne peuvent pas être identifiées avec ce que veut dire intuitivement le terme “être contenu dans” 154
159 Tout ce qu’on dit du soi-disant apprentissage, d’avoir quelque chose à faire avec les mains, avec le fait aussi bien de savoir se tenir à cheval ou sur des skis, ça n’a rien à faire avec ce qui est un savoir. Il y a un moment où vous vous dépêtrez avec des choses qu’on vous présente, qui sont des signifiants et, de la façon dont on vous les présente, ça ne veut rien dire; et puis, tout d’un coup, ça veut dire quelque chose, et ceci depuis l’origine. Il est sensible à la façon dont un enfant manie son premier alphabet que ce n’est d’aucun apprentissage qu’il s’agit mais de quelque chose qui est ce collapsus qui unit une grande lettre majuscule avec la forme de l’animal dont l’initiale est censée répondre à la lettre majuscule en question; l’enfant fait la conjonction ou ne la fait pas ; dans la majorité des cas, c’est-à-dire dans ceux où il n’est pas entouré d’une trop grande attention pédagogique, il la fait. Et le savoir, c’est ça. Et chaque fois que se produit un savoir, bien sûr, il n’est pas inutile qu’un sujet ait passé par cette étape pour comprendre ce qui se passera d’effet de savoir au niveau des petits schémas que j’ai un scrupule de ne pas vous avoir fait complètement bien sentir tout à l’heure, mais le temps me pressait, la théorie des ensembles. Nous y reviendrons s’il le faut.
Qu’est-ce que savoir ? Si nous devons, poussant les choses plus loin, interroger ce qu’il en est de cette analogie fondamentale, celle qui fait que le savoir ici reste encore parfaitement opaque puisqu’il s’agit au numérateur de la première relation d’un savoir singulier qui est ceci qu’il y a vérité, et parfaitement articulée à quoi il défaille en tant que savoir et que, en raison de cette relation, c’est de cette relation même que nous attendons la vérité sur ce qu’il en est du savoir. Il est clair que je ne vous laisse pas là au niveau d’une pure et simple énigme et que le fait que je l’ai introduit par ce terme a vous désigne que c’est effectivement dans l’articulation que j’ai déjà, me semble-t-il, assez cernée de l’objet a que doit tenir toute manipulation possible de la fonction du savoir.
L16, 17 (23.04.69), p.7 ; AFI p.221
Pour autant que la théorie des mathématiques, je ne dirai pas a abouti, car déjà on se glisse plus avant, mais tenons-nous en à ce qui en fait 221 l’équilibre de notre temps, la théorie des ensembles, nous constatons que l’essentiel de l’ordination numérique y est réduit à ce qu’il est, à ses possibilités articulatoires, et est construit pour le dépouiller cet ordre numérique de tous ses privilèges idéaux ou idéalisables, de ceux que j’évoquai comme je le pouvais à l’instant à vous réévoquer ce qu’était le Un, le Deux, voire tel ou tel nombre, dans une tradition que nous pouvons dire globalement gnostique, la théorie des ensembles précisément est faite pour dépouiller cette ordination numérique – et c’est ce que j’appelle de ces privilèges idéaux ou imaginaires – de l’unité – pas trace d’unité dans les définitions de Peano, un nombre se définit par rapport au zéro et à la fonction du successeur. L’unité n’y a aucun privilège – de l’unité, de la corporéité, de l’essentialité, de la totalité elle-même. Il faut bien marquer en ceci qu’un exemple ne saurait en aucune façon être confondu avec une classe ; et par tel autre trait comme ceci que parler de partie est profondément contraire au fonctionnement de la théorie, que le terme de sous-ensemble est très précisément fait pour montrer ceci qu’on ne saurait d’aucune façon y inscrire que le tout est fait de la somme des parties. Comme vous le savez, les sous-ensembles constituent de leur réunion quelque chose qui n’est nullement identifiable à l’ensemble, en le dépouillant même au fond, c’est là le sens de la théorie des ensembles, du recours à la spatialité elle-même.
L16, 21, p.5 (21.05.69) AFI p.271.
Cette substance du “ça se sait” instantané comme tel, s’accompagne de ceci qu’elle suppose que tout ce qui y attient, ça se sait, au sens de “ça se recouvre soi-même”, ça se sait dans son ensemble, c’est-à-dire que ce qui est révélateur, c’est que le supposé d’un discours qui aspire à pouvoir entièrement se recouvrir soi-même rencontre des limites. Il rencontre des limites en ceci précisément qu’il y existe des points qui n’y sont pas posables, dont la première image sera aussi bien donnée par la suite des nombres entiers et par ceci qui s’articule que celui défini comme étant plus grand qu’un quelconque n’y est justement pas posable, entendons dans cette série infinie, dit-on, des nombres entiers.
C’est précisément que ce nombre soit exclu, et proprement en tant que symbole, – nulle part ne peut être écrit ce nombre plus grand qu’aucun autre – c’est très précisément de cette impossibilité de l’écrire que toute la série des nombres entiers tire ce qu’elle a non pas d’être une simple graphie d’une chose qui peut s’écrire, mais d’être quelque chose qui est dans le réel. Cet impossible même est d’où surgit ce réel. Ce mécanisme est très précisément ce qui permet de le reprendre, au niveau du symbole, et d’inscrire au titre du transfini ce signe même non posable au niveau de la série des entiers, et de commencer à interroger sur ce qu’on peut opérer à partir de ce signe posé comme non posable au niveau de la série des entiers, et de s’apercevoir qu’effectivement ce signe, symbole repris au niveau de ce qui fait la réalité de toute la série des entiers, permet un nouveau traitement symbolique où les relations recevables au terme de la série des entiers peuvent être reprises, non pas toutes mais très certainement une part d’entre elles, et c’est le progrès qui se poursuit d’un discours tel que, pour se
savoir à chaque instant, jamais il ne se trouve sans rencontrer cette combinaison des limites avec ces trous qu’on appelle infini, c’est-à-dire non saisissable jusqu’à ce que justement il soit, d’être repris dans une structure différente, réductible à être cette limite, l’aporie en aucun cas n’étant que l’introduction à une structure de l’Autre.
C’est ce qu’on voit fort bien dans la théorie des ensembles, dans laquelle on peut un certain temps en effet s’avancer innocemment, et qui nous intéresse d’une façon particulière parce qu’après tout, au niveau plus
radical où nous avons à faire, à savoir de cette incidence du signifiant dans la répétition, en apparence rien n’objecte, rien n’objecte d’abord à ce que A ne soit que l’inscription entière de toutes les histoires possibles. Chaque signifiant renvoie d’autant plus à l’Autre qu’il ne peut renvoyer à lui-même qu’en tant qu’autre. Rien ne fait donc obstacle à ce que les signifiants se répartissent d’une façon circulaire, ce qui, à ce titre, permettra fort bien d’énoncer qu’il y a ensemble de tout ce qui de soi ne s’identifie pas à soi-même; à tourner en rond, il est parfaitement concevable que tout s’ordonne, même le catalogue de tous les catalogues qui ne se contiennent pas eux-mêmes. Il est parfaitement admissible, à cette seule condition qu’on sache, et c’est certain, qu’aucun catalogue ne se contient lui-même, sinon par son titre. Ça n’empêche pas que l’ensemble de tous les catalogues auront ce caractère clos que chaque catalogue, en tant qu’il ne se contient pas lui-même, peut toujours être inscrit dans un autre que lui-même contient. La seule chose exclue, si nous traçons le réseau de ces choses, c’est le tracé qui
s’écrirait ainsi, celui qui admet d’un
point à un autre d’un réseau quelconque et d’un réseau orienté, qui exclut, si b renvoie à un certain nombre d’autres points, d, e, f, qui exclut ceci que b renvoie à lui-même. Il suffit dans cette occasion que b renvoie à c, et que c lui-même renvoie à b pour qu’il n’y ait plus aucun obstacle à la subsistance corrélative de b et c et qu’une totalité les enveloppe.